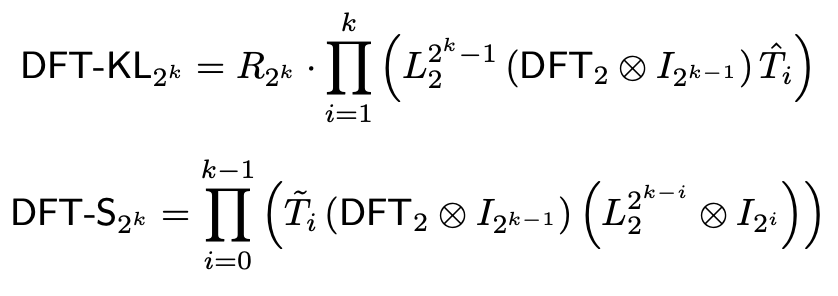
Comparative Analysis of the Vectorized Korn-Lambiotte and Stockham Fast Fourier Transforms: An Abstract Vector Machine Implementation

The Fast Fourier Transform (FFT) is a fundamental algorithm in computer science, enabling efficient computation of the Discrete Fourier Transform (DFT). Optimizing FFT performance is crucial for high-efficiency computing in applications like signal processing and homomorphic encryption. Our study focuses on designing and implementing vectorized FFT algorithms for large vector-length machines. We derive the vectorized formulas for the Stockham and Korn-Lambiotte FFTs from the iterative Cooley-Tukey, and compare their performance against each other based on memory and vector arithmetic operations to identify the most efficient approach for modern computational architectures.